Cómo ejecutar el algoritmo ABN de la resta (Detracción)
 En un artículo anterior «secuenciación en la introducción a la resta» se hablaba de la graduación a seguir para introducir esta operación. Ahora nos vamos a centrar en cómo realizarla mediante el algoritmo ABN, para lo cual empezaremos por la resta por «detracción».
En un artículo anterior «secuenciación en la introducción a la resta» se hablaba de la graduación a seguir para introducir esta operación. Ahora nos vamos a centrar en cómo realizarla mediante el algoritmo ABN, para lo cual empezaremos por la resta por «detracción».
Recordamos que esta operación les resulta especialmente difícil de aprender, básicamente por la existencia de cuatro situaciones distintas (aunque todas ellas se resuelvan con la misma operación) a las que hay que añadir los distintos tipos de situaciones problemáticas que se generan en cada una de ellas. (Para más detalle ver el artículo «Ejemplos de restas ABN«) Estas cuatro situaciones posibles son:
– Detracción: A una cantidad, quitar una indicadas y contar lo que nos queda.
– Escalera ascendente: Se parte de una cantidad a la que hay que añadir para llegar a otra.
– Escalera descendente: Se parte de una cantidad a la que hay que quitar para llegar a otra.
– Comparación: Hay que buscar en cuanto una cantidad es mayor o menor que otra.
OPERACIÓN POR DETRACCIÓN
Se presenta a continuación el procedimiento para la realización del algoritmo ABN para este tipo de situaciones. Las características del mismo son:
1.- Se separan tres columnas, nombrándolas «quito«, «quedan por quitar» y «restan«.
2.- Cada línea de la tabla representa un paso en la realización de la operación. Al igual que como se explicó en el algoritmo para la suma, el alumno realizará tantos pasos como considere oportunos. En este artículo se presentan varias posibilidades para una misma operación, pero existen tantas como las que crea oportunas cada niño.
3.- Recordamos, antes de continuar, que la principal característica de este método es que se adapta a las capacidades de cada alumno y por tanto no importa el número de pasos que necesite hacer, tampoco existen los términos «me llevo una» y que durante todo el proceso el alumno sabe cuanto le queda, cuanto ha quitado y cuanto resta aún por quitar.
4.- La columna «QUITO» se refiere a las cantidades que se van cogiendo del sustraendo (estas cantidades, reitero, dependen de como cada uno lo vea más fácil).
5.- La columna «QUEDAN POR QUITAR» refleja la cantidad del sustraendo que queda, tras quitarle la cifra de la primera columna. El último dato de esta columna será cero.
6.- La columna «RESTAN» es la cantidad que queda del minuendo al quitarle la cantidad de la primera columna. El último dato de esta columna será el resultado de la resta.
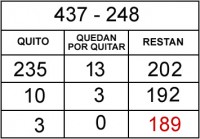
Veamos como se haría en una situación concreta, partiendo del siguiente problema: «En una pastelería se han elaborado 437 bollos de los que se han vendido, por la mañana, 248. ¿Cuántos bollos quedarán para la tarde?».
En este caso se han necesitado 5 pasos para llegar a la solución final.
– En la 1ª se han cogido 200 unidades del sustraendo (1ª columna), por lo que quedan 48 unidades del sustraendo (2ª columna) y restan 237 que es el resultado de quitarle al minuendo 437 los 200 que se han cogido en la primera columna.
– En la 2ª fila se ha decidido quitar 30 unidades del sustraendo (1ª columna) (si observas en la 1ª filaª 3 columna en el nº 237 hay 37 unidades), por lo que quedan por quitar 18 unidades del sustraendo y al restar los 30 del minuendo la 3ª columna queda con 207.
– En la 3ª fila se han quitado 7 unidades del sustraendo (1ª columna) (si observas en la 2ª filaª 3 columna en el nº 2o7 hay 7 unidades. La mayoría del alumnado hasta que no cogen soltura les cuesta pasar de centena y decena), por lo que quedan por quitar 11 (nos quedaban 18 menos los 7 que hemos cogido) y al restar los 7 en el minuendo la 3ª columna queda con 200.
– En la 4ª fila se han quitado 10 (1ª columna), por lo que quedan por quitar 1 (2ª columna) y al restar los 10 en el minuendo la 3ª columna queda con 190.
– En la última fila quitamos la unidad que nos queda, con lo que la 2ª columna queda a cero y la última refleja el resultado final.
Resumiendo: La primera columna va reflejando las cantidades que se van cogiendo del sustraendo (dichas cantidades las decide quién realiza la operación) y la 2ª y 3ª columna reflejan las cantidades que quedan en el sustraendo y en el minuendo respectivamente.
Otro ejemplo, resuelto en tres pasos, sobre la misma cuenta
En este último la destreza en el cálculo adquirido le permite solucionarlo en sólo dos pasos.
Para saber más : Martínez Montero, J. (2010). ENSEÑAR MATEMÁTICAS a alumnos con necesidades educativas especiales. 2ª Edición. Madrid: Wolters Kluwer



Deja una respuesta