Cómo ejecutar el algoritmo ABN de la resta (Escalera ascendente)
 Continuo con este artículo explicando cómo ejecutar la resta mediante el algoritmo ABN mediante la «Escalera ascendente», segunda de las cuatro posibilidades que tiene esta operación matemática.
Continuo con este artículo explicando cómo ejecutar la resta mediante el algoritmo ABN mediante la «Escalera ascendente», segunda de las cuatro posibilidades que tiene esta operación matemática.
Dentro de este epígrafe se encuentran dos tipos de problemas, en los que partiendo de una cantidad debemos llegar a una mayor también conocida y determinar esa diferencia. Ejemplos de estos dos tipos de problemas son:
– Cuando empezaron el partido había 6 niños jugando y cuando acabaron había 12. ¿Cuántos niños se añadieron al juego?.
– En un cesto María ha recogido 8 manzanas y su hermano Pepe 5. ¿Cuántas manzanas tienen que recoger Pepe para tener las mismas que María?.
Respecto a la forma de resolverlo, mediante el algoritmo ABN, sólo necesitamos dos columnas, en la primera ponemos la cantidad que vamos poniendo (podemos nombrarla como «AÑADO») y
en la segunda (podemos nombrarla como «LLEGO A») iremos poniendo las sumas parciales que alcanzamos al añadirle al sustraendo las cantidades que cada alumno/a ha ido poniendo en la primera columna, hasta llegar a la cifra del minuendo. En ese momento se suman las cantidades de la 1ª columna que será el resultado. Al final del artículo he puesto un vídeo que ilustra por un alumno este tipo de operación.
Al igual que en las anteriores operaciones que hemos explicado mediante este método, las cantidades que se van cogiendo las elige cada uno en función de su habilidad en el cálculo, por lo que una misma operación podrá tener tantos pasos como necesite el niño/a.
También y gracias a la flexibilidad y adaptación del método, el que realiza la operación puede elegir si poner en la primera fila el sustraendo al objeto de continuar a partir del mismo añadiendo cantidades.
Veamos en varios ejemplos de la misma operación cómo se desarrolla el algoritmo ABN de la resta en escalera ascendente.
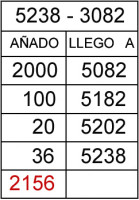
Primer ejemplo: 5238 – 3082
1.- En la 1ª fila se ha añadido 2000 en la 1ª columna y en la segunda se ha puesto 5082 (resultado de sumarle al sustraendo 3082 las 2000 añadidas).
2.- En la 2ª fila se ha añadido 2100 en la 1ª columna y en la segunda se ha puesto 5182 (resultado de sumarle a la inmediatamente superior 5082 las 100 añadidas).
3.- En la 3ª fila se ha añadido 20 en la 1ª columna y en la segunda se ha puesto 5202 (resultado de sumarle a la inmediatamente superior 5182 las 20 añadidas).
4.- En la 4ª fila se ha añadido 36 en la 1ª columna y en la segunda se ha puesto 5238 (resultado de sumarle a la inmediatamente superior 5202 las 36 añadidas), con lo cual hemos llegado a la cifra del minuendo y hemos acabado de añadir, ya sólo queda sumar la primera columna para saber el resultado.
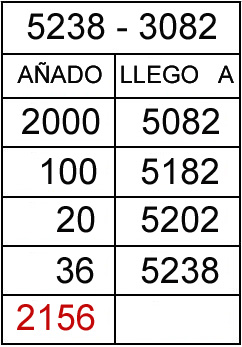
Segundo ejemplo: 5238 – 3082
En este ejemplo no se detalla el desarrollo (si lo precisas indícalo en los comentarios) el desarrollo ha precisado un paso menos (estos dependen de la agilidad en el calculo de cada persona).
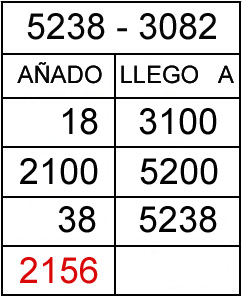
Tercer ejemplo: 5238 – 3082
En este tercer ejemplo se ha cambiado la cabecera y se a añadido en la primera fila justo debajo de la cabecera el sustraendo al que se le irá añadiendo las cantidades de la primera columna. El diseño del formato depende también de los gustos y necesidades del que opera, el resto del procedimiento es el mismo descrito anteriormente.
NOTA IMPORTANTE:
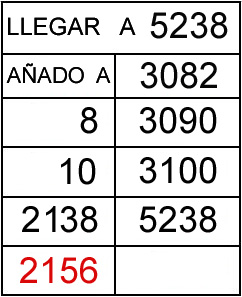
Cuando un alumno/a trabaja el algoritmo ABN, el término «me llevo…» no existe, por tanto no hay sumas y restas llevando y sin llevar, sólo son sumas y restas. Cuando una persona que ha aprendido con el método tradicional tiene que sumar la 1ª columna ( 8 + 10 + 2138) lo normal (a ti te pasará) es que diga 8 y 8 son 16, pongo 6 y me llevo 1.
Un alumno/a que trabaja el algoritmo ABN tras trabajar la numeración y la suma mediante este método, lo que hace es buscar mentalmente las combinaciones posibles para formar decenas, centenas,… por lo que nunca necesitará llevarse una.
En el ejemplo anterior de lo que podría hacer con la suma anterior podría ser así:
A 8 le quito 2 que lo sumo a 38, hace 40 + 10 serían 50 que con los 6 iniciales quedarían 56 que formaría el 2156.
Que aunque te parezca más complicado, sería una operación mental a la cual está acostumbrado y la realizaría más rápidamente y con una mayor comprensión de las operaciones que está haciendo.
VÍDEO QUE ILUSTRA ESTA OPERACIÓN
El alumno es de 2º de primaria del CEIP Andalucía de Cádiz
Para saber más : Martínez Montero, J. (2010). ENSEÑAR MATEMÁTICAS a alumnos con necesidades educativas especiales. 2ª Edición. Madrid: Wolters Kluwer

Deja una respuesta