La cadena numérica
 Segunda entrega del capítulo dedicado a la «acción de contar». Puedes ver ejempos para trabajar en clase sobre este artículo en «cadena numérica«).
Segunda entrega del capítulo dedicado a la «acción de contar». Puedes ver ejempos para trabajar en clase sobre este artículo en «cadena numérica«).
2.1. La cadena numérica
Contar, numerar, hallar cardinales, subir o bajar por sucesiones de números, etc., requiere la posesión de la cadena numérica y capacidad para verbalizarla de manera correcta. Aprender los nombres de los números, su sucesión, sus normas de construcción, es algo ineludible y una de las primeras tareas a las que se enfrenta el niño nada más traspasar el umbral de la escuela. Ahora bien, este aprendizaje no se hace de una vez. No es de los que o se saben o no se saben, ni de los que no admiten grados de aproximación. Admite matizaciones y fases de progreso. Hace ya años Fuson y Hall establecieron que en el dominio de la cadena numérica el niño pasa por cinco niveles de progresión. Son los que siguen:
- NIVEL CUERDA. En este nivel se encuentra el alumno que es capaz de recitar un trozo de la secuencia numérica empezando a partir del número 1 y sólo del número 1. Los nombres de los números son recitados por evocación. El sonido de lo que está diciendo trae encadenados los sonidos siguientes, de una manera parecida a como antes el pueblo sencillo cantaba en latín. No hay diferenciación ni fronteras entre un número y otro. Este conocimiento verbal no puede aplicarse al conteo. Incluso el niño está excesivamente pendiente de lo que dice, lo que le impide llevar a cabo otras tareas. Es el nivel más elemental, y en el que suelen ser iniciados los niños en sus casas desde tempranas edades. Con poco más de dos años ya es el niño capaz de decir algunos números en cadena, aunque naturalmente esto no pasa de ser una “gracia”. En este nivel, el niño no llega a comprender el sentido de la acción de contar. Cree que consiste en recitar los nombres de los números y, al mismo tiempo, señalar los objetos que se cuentan. Evidentemente, sin establecer una correspondencia mínimamente exacta entre lo que se dice y lo que se señala. Así, el sujeto puede decir dos números mientras señala un objeto, señalar dos objetos, pero asignándole sólo un número, o seguir recitando números aunque se acaben los objetos, o, finalmente, seguir señalando objetos aunque haya dejado de decir nombres de números.
- NIVEL CADENA IRROMPIBLE. Hay poca diferencia con el nivel anterior y, sin embargo, se deben realizar muchos ejercicios y mucho entrenamiento para acceder a este nuevo nivel. El alumno, para empezar a contar, debe comenzar siempre en el uno. Si no lo hace así no es capaz. Parece como si al empezar el niño su aprendizaje en una destreza nueva no almacenara nada, o, dicho en términos muy gráficos, “se le vaciara todo el agua”. Tienen que pasar muchos ejercicios para que el alumno parta de lo conocido. Por ejemplo: cuando cuenta cuántas son 5 y 3, extiende todos los dedos de una mano y tres de la otra. Naturalmente, cuenta los cinco dedos de la mano, aunque sepa que tiene cinco. Si el ejercicio siguiente es averiguar cuántas son 5 y 4, el niño de 5-6 años actuará de la misma manera. Pero, por contraposición al nivel anterior ya tiene bien diferenciados los números, sabiendo dónde acaba uno y dónde empieza otro. Adquirido este nivel, o, para ser más exactos, llegado el alumno a este nivel, puede comenzar las tareas de contar con posibilidades de éxito. Gracias a ello, realizará muchos ejercicios que le permitirán pasar al escalón siguiente.
- NIVEL CADENA ROMPIBLE. Supone un salto notable con respecto al nivel anterior. Aquí el alumno es capaz de ‘romper’ la cadena, comenzando a contar a partir de cualquier número que se le indique. El niño que es capaz de cumplir la orden: «Cuenta a partir del número…», se encuentra en este nivel.
- NIVEL CADENA NUMERABLE. Este nivel supone un dominio notable de la sucesión numérica. El niño es capaz, comenzando desde cualquier número, de contar un número determinado de eslabones y detenerse en el número que corresponda. El niño que, por ejemplo, es capaz de contar 8 números a partir del 3 y decir en qué número ha terminado, ha alcanzado este nivel. Desde este dominio, se afrontan con bastantes garantías la realización de las operaciones básicas del cálculo. También se ha de tener presente que este escalón supone un salto en dificultad muy apreciable y que, por ello, en el caso de los niños con dificultades, debe conllevar un proceso de aprendizaje muy reforzado y con ayudas de todo tipo.
- NIVEL CADENA BIDIRECCIONAL. Es el máximo dominio al que se puede llegar. En esencia, supone las destrezas del nivel anterior aplicadas hacia arriba o hacia abajo, e incrementando notablemente la velocidad. Contar desde 11 ocho números hacia abajo en aproximadamente el mismo tiempo que hacia arriba y contestar exactamente el número que alcanza, es una tarea que define al alumno que ha alcanzado este nivel.
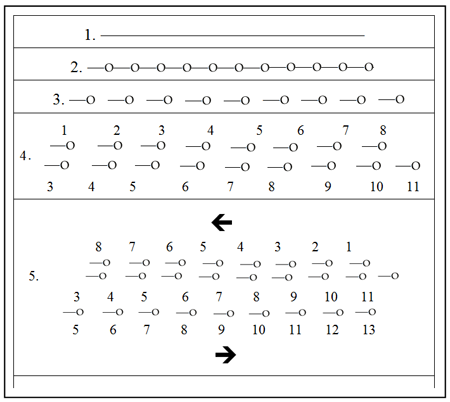
La siguiente figura muestra lo que se quiere señalar.
INDICE DE ARTÍCULOS PUBLICADOS
1. – Introducción
2.- Las fases de la progresión en la cadena numérica.
2.1.- La cadena numérica
2.2.- Secuenciación para la adquisición de los primeros niveles de la cadena numérica.
2.2.1.- Avisos sobre las actuales prácticas.
2.2.2.- La disposición de los objetos a contar.
2.2.3.- Ejercicios y actividades para el dominio de los niveles dos y tres de la cadena numérica.





Deja una respuesta