Esta ilusión geométrica apareció en el blog «gaussianos.com» vía «Futility Closet».  Se trata del mismo efecto  del que nos hicimos eco hace un tiempo en «¿Dónde está el trozo que falta?» , con un triángulo rectángulo que representa una clásica ilusión llamada la «Paradoja del cuadrado perdido»  (Ver animación).

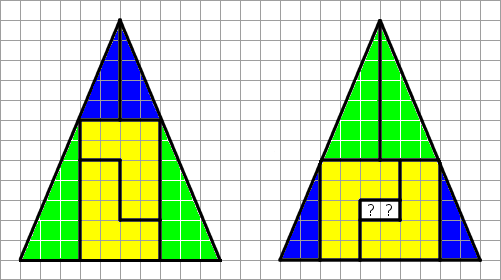
En ésta ocasión consiste en dividir un triángulo en 6 piezas como en la figura de la izquierda. Después re ordenamos como en la figura de la derecha…y vemos que aparece un espacio sin rellenar. Es decir, tras el cambio la figura resultante es más pequeña que la primera…

La explicación la dejamos al final del artículo. (Ver animación)

Ver el desarrollo del problema con piezas recortadas.

Sí son exactamente iguales. La explicación está en cuestiones milimétricas que se desprecian y que al hacerse grande dan la cara. Para entenderlo mejor debemos ver que el error está en suponer que la figura inicial es un triángulo, error producido por:

1.- El sentido común, con el que regularmente asumimos las diferencias pequeñas como despreciables. Vemos la imagen inicial y damos por supuesto que es un triángulo perfecto, cuando no lo es, así como despreciar igualmente el grosor de los bordes, como si estos no existiesen.
2.- El grosor de línea, que es casi similar al “grosor” de los triángulos de área 0,5.
3.- La cuadrícula, que tiende a proveer un pequeño camuflaje para esos vértices de ángulos de casi 180º.

4.- La inclinación de los triángulos también induce un pequeño error despreciable. En nuestro caso en concreto en un pequeña inclinación de los triángulos. La del 3×7 no es la misma que la del 2×5. En el caso del de 2×5 el ángulo de la base es de 68.198 grados mientras que en el de 3×7 es de 66.8.

La suma de estas diferencias en la figura (que no triángulo)  que no se ven fácilmente a simple vista son las que se muestran en el hueco. Si prescindimos del engaño visual y lo demostramos matemáticamente, vemos que si se cumple la exactitud entre ambas figuras.

Si damos a cada cuadro un lado 1 cm, el área teórica de cada triángulo sería 12*10/2=60 cm2

Haciendo la cuenta por figuras geométricas en el de la izquierda nos da un total de 59 cm2:

– Triángulos azules  2*5/2*2= 10 cm2

– Triángulos verdes  3*7/2*2= 21 cm2

– Polígonos amarillos 7*4= 28 cm2

Lo que dá un total de 59 cm2.

El de la derecha tendría 59+2=61 cm2. Una pequeña variación que ópticamente no se aprecia.