El lenguaje y el m.c.m. y el m.c.d.
Atentos al lenguaje «claro y conciso» de las definiciones que hemos oido una y otra vez sobre el máximo común divisor y el mínimo común múltiplo y para ello partimos del consabido: «Partiendo de 2 o más números y por descomposición en factores primos, expresados como producto de factores primos…»
«…su mínimo común múltiplo será el resultado de multiplicar todos los factores comunes y no comunes elevados a la mayor potencia»
«… el máximo común divisor será el resultado de multiplicar los factores comunes elevados a la menor potencia».
Para un matemático esto no tiene vuelta de hoja, pero para mi, como docente, reconozco que en más de una ocasión cuando he tenido que explicarlo le he echado una mirada porque tras un tiempo sin trabajar, y sin pararme a pensarlo debidamente, no me sentía seguro de quién era quién. Lo queramos ver como lo queramos ver para el alumnado este tipo de definición, aunque exacta, es fácil confundirla si no se tiene suficiente capacidad de razonamiento suficiente para deducir por lógica.
Jose Luís García González, maestro en Cantabria, a raíz de los artículos sobre cálculo manipulativo del de m.c.m. y m.c.d. con cartas o con piezas de construcción,me comenta que tradicionalmente, la forma que se nos enseñaba para calcularlo no es más que una receta mecánica: «Descomponer en factores, y luego coger los factores comunes con su menor exponente». La receta, ciertamente funciona, pero carece de sentido para el alumnado y con ella se recorre a un procedimiento mecánico para obtener un resultado.
Por ello propone un enfoque más al estilo ABN de dotar de sentido a los cálculos matemáticos, y nos propone explicar el MCD según la alternativa que existe para obtenerlo.
1.- Calculamos los divisores de cada número y elegimos el común mayor a ambos. Por ejemplo, M.C.D. de (8, 12)
Divisores de 12: 1, 2, 3, 4 y 12.
Divisores de 8: 1, 2, 4 y 8.
Por tanto el M.C.D. (8, 12) = 4
2.- Y para el M.C.M. ahora les pediremos que calculen los múltiplos de ambos números y luego escojan el menor de los comunes a ambos. Por ejemplo para el M.C.M. de (8, 12)
Múltiplos de 12: 24, 36, 48…
Múltiplos de 8: 16, 24, 32…
Por tanto el M.C.M.(8, 12) = 24
Evidentemente si nos planteamos dos número o más, que tengan muchos divisores o cuyos múltiplos comunes no coincidan hasta un elevado número de múltiplos, nos podrían dar las uvas. Pero la pregunta sería ¿trabajamos en clase con esos números tan grandes o son números más sencillos con los que nos manejamos para llegar al que buscamos?.
Personalmente creo que en esta cuestión el tema no está en el procedimiento en sí para encontrar el m.c.m. y el m.c.d, sino en que el alumnado entendienda qué sentido real tienen y para qué sirve conocerlos. Para ello un lenguaje claro y una metodología ágil y sencilla hará más comprensible que el alumnado adquiera esos conceptos y su utilidad práctica en situaciones de la vida real. Más adelante habrá tiempo de sistematizar aprendizajes más complejos.
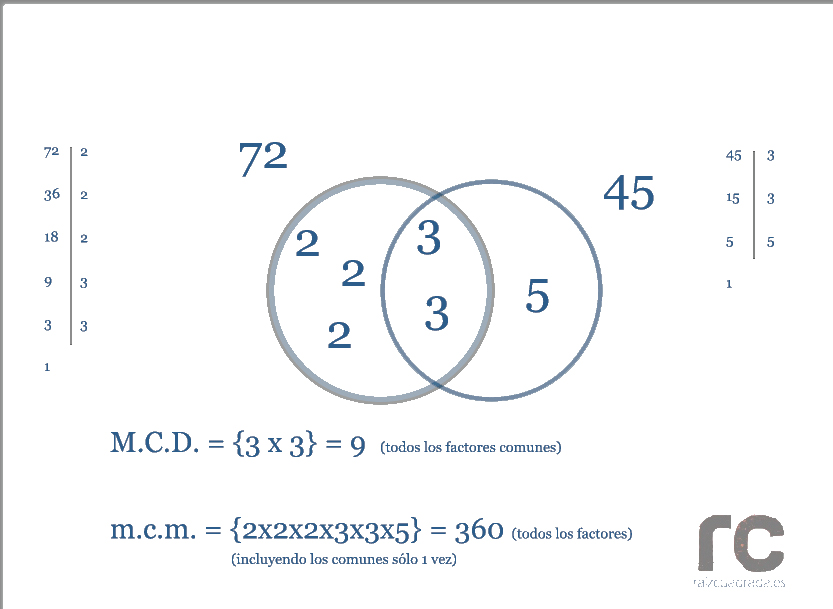
Fuente imagen: «Raiz cuadrada«
Este contenido se publicó por primera vez en actiludis.com el 08/11/2016





Deja una respuesta