En esta actividad se trabaja el cálculo reflexivo ya que no sólo se calcula, sino que además hay que buscar una estrategia para resolver la cuadrícula de forma que las distintas combinaciones cuadren con el número 13.6. Para los que trabajamos el método ABN esta actividad se puede plantear también como la realización de la resta en escalera

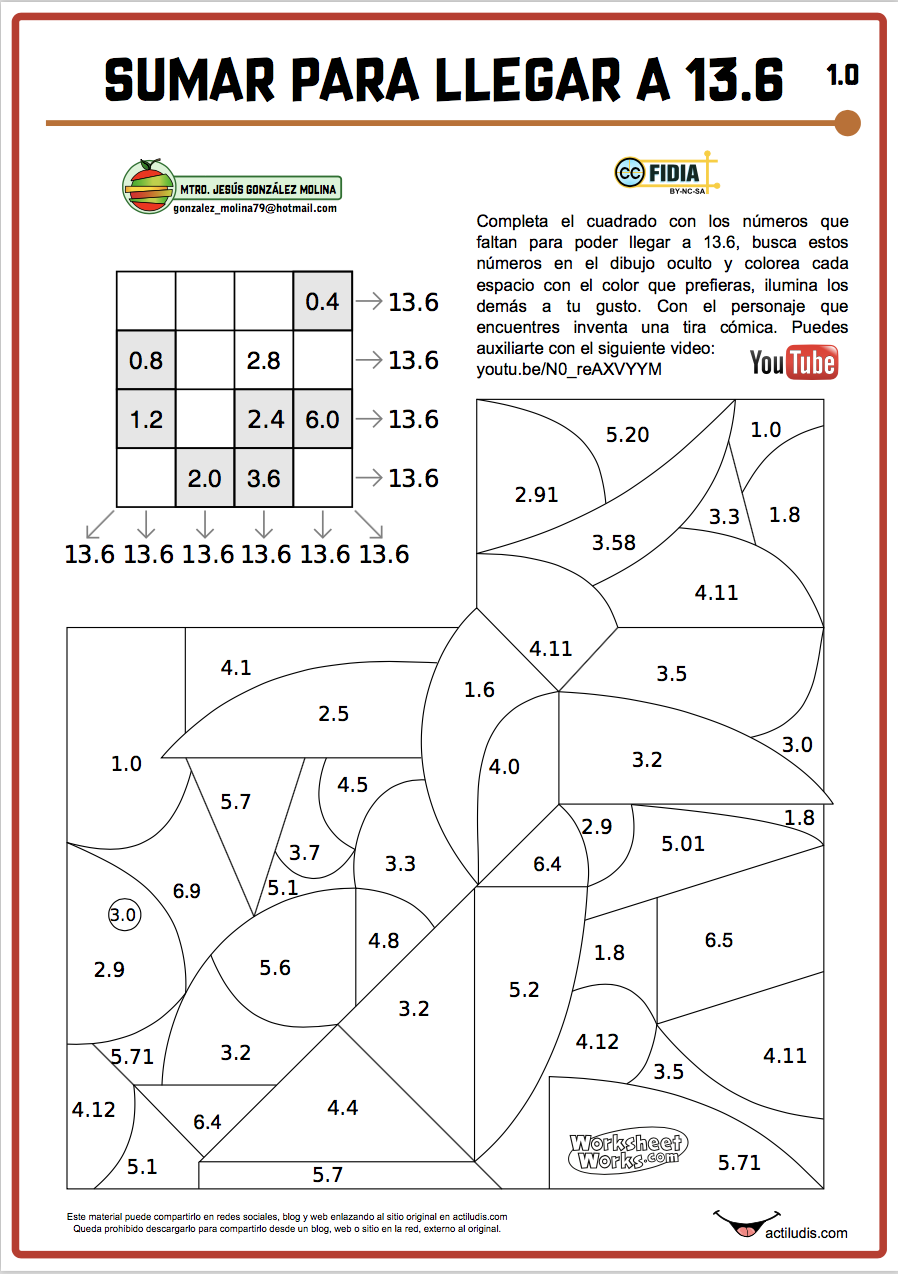
Para completar el cuadrado puede empezar buscando el dato de la suma que más completa del la cuadrícula. Una vez resuelto debe  buscar estos números en el dibujo oculto y colorear cada espacio con el color que prefieras para descubrir el dibujo oculto.

Por último  como propuesta se pide que con el personaje que encuentre invente una tira cómica y se aconseja el visionado del vídeo «Cómo dibujar tiras cómicas» que hay al final de este articulo.

El autor de este material es el profesor Jesús González Molina de la Escuela Primaria Vicente Guerrero y catedrático en el nivel de posgrados, desde Los Placeres del Oro, en el estado de Guerrero, México.

DESCARGAR: «SUMAS PARA LLEGAR A 13.6«

DESCARGAR: «SOLUCIÓN«