He visto la siguiente operación en el Facebook del grupo ABN la cual apareció en una de las pruebas de la Comunidad Autónoma de Castilla León. He leído los comentarios y no puedo estar más de acuerdo con aquellos que critican poner tal absurdo en una prueba que tiene como fin determinar el grado de competencia matemática para la vida ordinaria de nuestro alumnado, y de la cual destaco la reiterada aportación de Jaime Martínez Montero, así como también no puedo dejar de hacer mención la acertada pregunta que se hace mi querido amigo Juanma Garrán: “¿Qué estándar de aprendizaje evaluable es el referente para dicho ejercicio?” Pero no puedo dejar pasar de lado, la opinión de quien afirma, a pesar de reconocer no haber revisado a fondo el método, que el método ABN tiene lagunas.

Por ello partiendo de la afirmación de que esta operación no tiene más valor que el mero entretenimiento lúdico y está muy lejos de ser un contenido educativo exigible, me he puesto a resolverla exclusivamente con los conocimientos ABN que los niños conocen. Los pasos seguidos han sido:

1.- La suma del minuendo o el sustraendo con la resta o diferencia nos dará el otro elemento de la resta que no estemos sumando. De ahí que podemos expresar la operación inversa de la siguiente forma  (las cifras que faltan se representan con el guion bajo):

12 430 + _ 3 4 7 _=  4 _ 9 _ 5

2.- Sumo primero la parte que conozco de _347_. Evidentemente, esto lo podré hacer paso a paso, con las cantidades numéricas que me sean más sencillas o de una sola vez, para eso estamos en un algoritmo abierto que se adapta a cada persona. En mi caso he cogido el número 347 que es una parte del total.

 

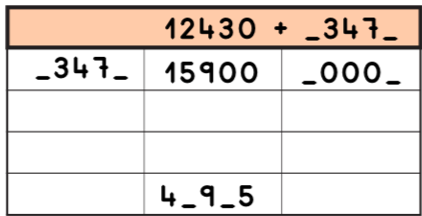
3.- Con la simple observación de lo que ya tenemos y lo que nos falta es sencillo completar los huecos. Lo haré en varios pasos para que se vea mejor.

4.- Como el resultado de la suma 4 _ 9 _ 5, tiene un 5 en la cifra de las unidades está claro que esa es la cifra de las unidades en _345_

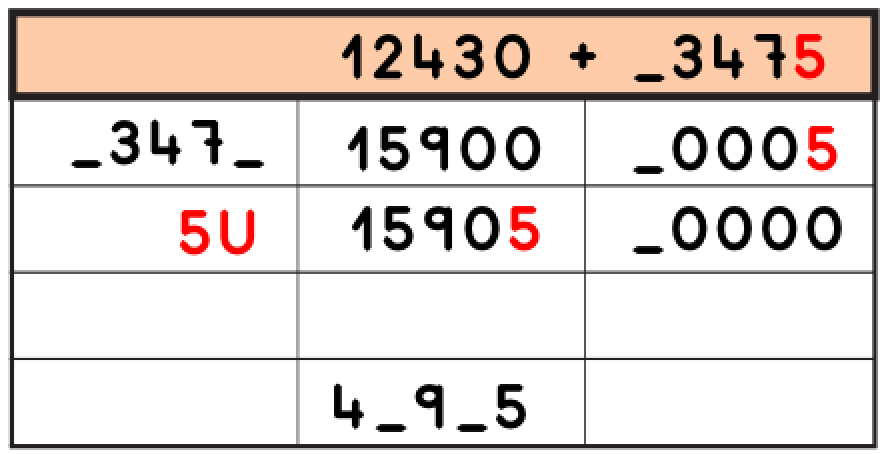
5.- Continuando con la observación vemos que la cifra de las decenas del resultado no puede ser otra que el cero ya que no tenemos ni cifra de U ni D que sumarle. Por tanto ya llevamos dos cifras averiguadas en los números.

6.- Seguimos observando y vemos que tampoco tenemos cifra de Unidades de Millar que sumar a 15905, por tanto, la cifra de las Unidades de Millar en 4_905 tiene que ser el 5. Ya hemos completado uno de los números 45 905.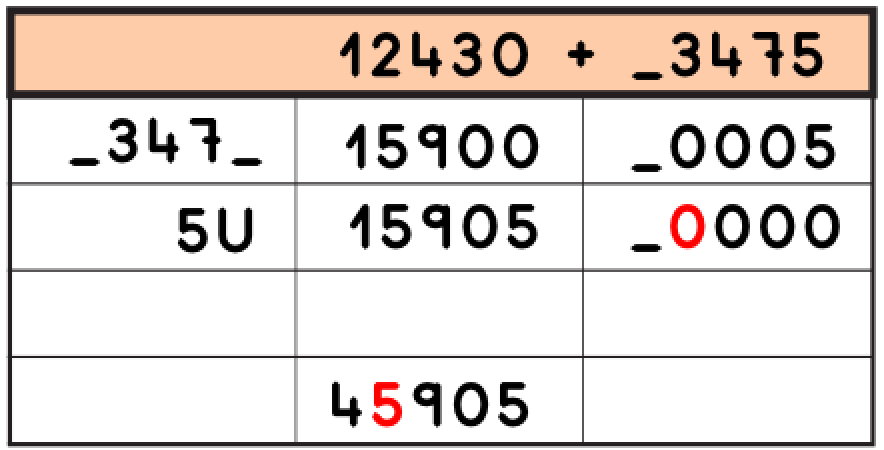

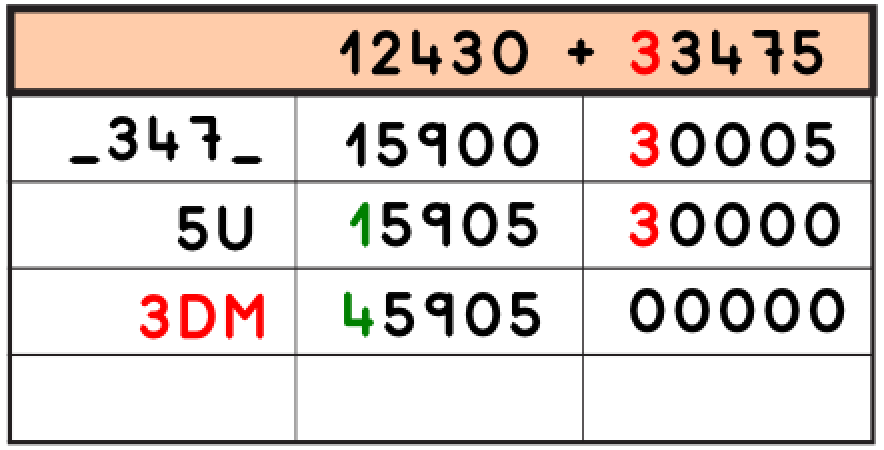
7.- Por último, queda averiguar las Decenas de Millar del _3 475. Para ello basta mirar las DM de 15 905 y de 45 905 para ver que son 3DM el dato que nos falta.

CONCLUSIÓN

Como entretenimiento lúdico está muy bien, de hecho, cuando trabajaba el método tradicional hice algunas fichas para que el alumnado jugara con ello, pero jamás se me ocurrió ponerlo como contenido a evaluar… y queda demostrado que no hay lagunas en el ABN.