El lado oscuro del proyecto de currículum de matemáticas en Primaria
«EL LADO OSCURO DEL PROYECTO DE CURRÍCULUM DE MATEMÁTICAS EN PRIMARIA» es el título de un interesantísimo artículo de Jaime Martínez Montero, que analiza lo que el ministerio de educación ha elaborado y que las CCAA tomarán como referente de mínimos para elaborar los suyos propios. Este artículo lo podéis descargar en PDF desde el blog original den «Algoritmos ABN».
Sin lugar a dudas un documento necesario conocer, tanto se haya leido el currículum de la nueva ley, como si aún no lo has hecho. Aquí reproducimos el artículo y os invitamos a descargarlo para su estudio y reflexión.

Por Jaime Martínez Montero.
En mi anterior artículo «¿Hay ABN en el proyecto del currículum de matemáticas» me ocupaba de algunos contenidos del proyecto que analizamos que podían ser inspirados (o que encajaban) con el método ABN. En el presente artículo voy a tener que ocuparme del “lado oscuro” del proyecto, es decir, las insuficiencias, los vacíos, los sinsentidos o los errores. Para no alargar en exceso este texto, lo voy a dividir en tres partes. En la primera analizaré algunos de los contenidos que están “puestos” en dicho proyecto. En la segunda señalaré las ausencias inesperadas o sorpresivas de contenidos. Finalmente, haré algunas valoraciones sobre el documento desde un punto de vista global.
ANÁLISIS DE ALGUNOS SABERES BÁSICOS CONTENIDOS EN EL PROYECTO DE CURRÍCULUM.
PRIMER CICLO.
“Estrategias variadas de conteo y recuento sistemático en situaciones de la vida cotidiana en cantidades hasta el 199.”
No se entiende la razón por la que la progresión en el conocimiento de los números se detenga, al final del segundo curso, en el 199. Trasluce la idea de que los números se aprenden de uno en uno. Está bastante establecido que en 1º los niños trabajen a fondo las decenas y en 2º las centenas. En este caso no van a poder trabajar más que una centena (¿?) y de manera incompleta. Si por ejemplo llegaran hasta el 200 se facilitarían mucho las descomposiciones, sería fácil hallar las mitades, la mitad de la mitad y la mitad de la mitad de la mitad. También lo sería establecer los amigos del 200, y extender a esa centena lo que ya sabían hacer en 1º. El número 199 es un número primo, por lo que su descomposición es más difícil: en el ámbito de los números naturales no se pueden hallar mitades, tercios, cuartas, quintas o décimas partes, etc. Por otro lado, se traslada la idea de que el número 200 solo puede estar formado por dos centenas. Pues no, puede estar formado por una centena y diez decenas, o por veinte decenas, o por cinco decenas y ciento cincuenta unidades, etc. En fin, o es algo incomprensible o se han utilizado argumentos que no se conocen.
Estrategias y técnicas de conteo en 1º de Primaria.
“Estrategias y técnicas de construcción de formas geométricas sencillas de una,
dos o tres dimensiones de forma manipulativa.”
No me he podido resistir a hacer notar lo especiales que deben ser las estrategias y las técnicas que permitan la construcción de una figura de una dimensión. Claramente es un error material, pero su aparición en el documento denota que el mismo no se ha corregido de forma cuidadosa.
SEGUNDO CICLO.
“Estrategias variadas de conteo, recuento sistemático y adaptación del conteo al tamaño de los números en situaciones de la vida cotidiana en cantidades hasta el 9999”.
Aquí se puede aplicar todo lo dicho en el Primer Ciclo respecto al número 199. Incluyendo los vídeos.
“Fracciones propias con denominador hasta 10 en contextos de la vida cotidiana.”
Se limita muchísimo el ámbito de trabajo con los números fraccionarios. ¿Por qué no se llega a la fracción unidad, que permitiría entender mejor las fracciones propias y sería el paso a las fracciones impropias? Se hace mención a la vida cotidiana, pero ¿acaso no es cotidiano el kilo y cuarto, el litro y medio, el metro y medio? Ocurre con esto como con otros contenidos. Se conceptualizan mejor cuando se pueden contraponer a otros distintos de su misma categoría. Es el caso de las fracciones propias contrastadas con las fracciones impropias, y viceversa. Si no hay fracciones impropias habrá que abandonar los números mixtos y todas las posibilidades que ofrecen. Entre otras reduce las posibilidades de expresión de una cantidad, reduce el ámbito de resolución de problemas, respecto a los porcentajes no se podrán expresar en fracción los aumentos porcentuales: si se ha subido un producto el 20%, se puede expresar como 120% o de una forma más comprensiva: 1 1/5. Etc.
“Estrategias de cálculo mental con números naturales y fracciones.”
Respecto a las estrategias de cálculo mental, que es algo que se repite mucho, se podría haber sido más explícito. No parece sensato que se emplee la misma expresión para los niños de 6 a 8 años que para los de 10 a 12. Y respecto al cálculo mental con fracciones propias con denominador menor de diez, pues la verdad es que se puede hacer muy poquito. En primer lugar, porque no se trabaja ni la suma ni la resta con fracciones. Y en segundo lugar, porque, si se trabajara, enseguida se acabarían los ejercicios. En las sumas de fracciones de denominador 3 solo se puede sumar 1/3 con 1/3. En las denominador 6 solo caben las sumas en las que las parejas de numeradores sean 4 y 1, 3 y 2, 2 y 3, 1 y 4, más los numeradores que sumen cuatro, tres y dos. En resumidas cuentas, no se trataría más que de combinaciones de sumas apropiadas para le Educación Infantil… de tres años.
“Números naturales y fracciones en contextos de la vida cotidiana: comparación y ordenación.”
¿Cómo se compara un número natural con una fracción propia?
“Atributos mensurables de los objetos (longitud, masa, capacidad, superficie, volumen y amplitud del ángulo).” Más adelante se mencionan las unidades convencionales: “Unidades convencionales (km, m, cm, mm; kg, g; l y ml) y no convencionales en situaciones de la vida cotidiana.” De un párrafo a otro se han “caído” las unidades de superficie. Respecto a las unidades de peso, el hectogramo, los cien gramos, es en la vida cotidiana, a la que tanto se apela, bastante más común que el gramo. Pero el problema es otro. Si, como en el caso de la longitud, se omiten los hm y los dam, ¿se va a poder entender la estructura a la que se ordenan las distintas medidas y que es idéntica al sistema de numeración decimal? ¿Qué tipo de números incomplejos se van a formar en las unidades de capacidad, donde solo hay litros y mililitros? Finalmente, el currículum olvida las unidades agrarias. Puede estar justificado en parte. Pero una de ellas es muy frecuente, se utiliza con profusión y es la unidad de medida de superficies que aparece en los medios de comunicación. Hablamos de la hectárea.
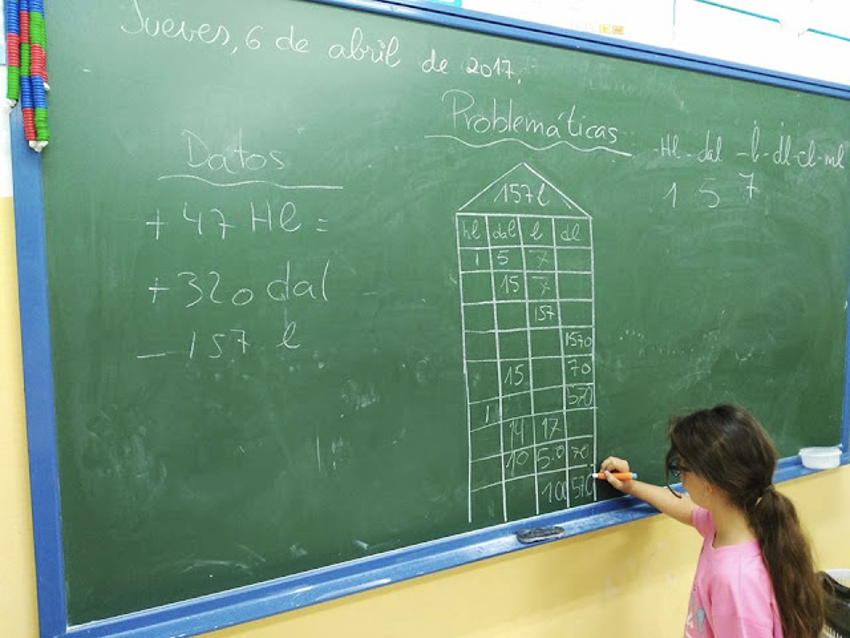
“Modelos geométricos en la resolución de problemas relacionados con los otros sentidos.”
Esta redacción, que aparece en más ocasiones, debería ser mejor explicada, porque no se sabe a qué sentidos hace referencia.
“La moda: interpretación como el dato más frecuente.”
No se debería tratar como único estadístico. Alcanzaría más sentido con la mediana, y también con le media. ¿Por qué no se incluyen ambos valores? Respecto a la media, no se ve dónde está el problema por el cual los niños sumen unos datos (normalmente de una o dos cifras) y el resultado lo dividan por el número de casos. Como tampoco se entiende que el rango de una distribución, o sea, sencillamente la diferencia que exista entre el valor más alto y el más bajo, se tenga que dejar para el Tercer Ciclo. No existe demasiada confianza en las capacidades de los alumnos.
4º de Primaria. CEIP “San Rafael”, de Cádiz.
TERCER CICLO.
“Números naturales, fracciones y decimales hasta las milésimas en contextos de la vida cotidiana: comparación y ordenación.”
¡Vaya salto! Los números naturales se pueden trabajar sin límites, mientras que en el 2º Ciclo se tenían que parar los alumnos en el 9999. Es decir, que van aquí las decenas de mil, las centenas de mil y los millones. Las fracciones parece que se abordan en su totalidad: propias e impropias, números mixtos, etc. ¿Y los decimales? Pues se pasa de no citarlos a llegar hasta las milésimas.
“Potencia como producto de factores iguales. Cuadrados y cubos.”
No se termina de entender. ¿Quiere decir que se trabajan las potencias sin límites y que, además, hay que prestar especial atención a los cuadrados y a los cubos? ¿O que sólo hay que trabajar los cuadrados y los cubos? Respecto a estos últimos (los cubos) no se sabe para qué se trabajan ni la utilidad que pueden tener los mismos. Lo digo porque no se estudian las unidades de volumen ni los volúmenes de los cuerpos. Evidentemente, para qué vamos a hablar de raíces cúbicas.
“Identificación de un conjunto de datos como muestra de un conjunto más grande y reflexión sobre la población a la que es posible aplicar las conclusiones de investigaciones estadísticas sencillas.”
Es decir, que los alumnos se inician en la estadística inferencial. Esto sí que es un salto de gigante. Sinceramente se queda uno desconcertado, y más con el escaso trabajo estadístico realizado con anterioridad y con las débiles herramientas de cálculo adquiridas. La propia redacción causa extrañeza. En primer lugar, que los alumnos sean capaces de identificar un conjunto de datos como una muestra de un conjunto más grande es ir al revés. Normalmente se tiene a la población y, en función de sus características y de lo que se quiera investigar se elabora la muestra. En segundo lugar, que los alumnos reflexionen sobre la población a la que es posible aplicar las conclusiones es también poner el carro delante de los bueyes: tras la reflexión se podrá establecer que es posible aplicar las conclusiones… de investigaciones estadísticas sencillas que no se hacen con la muestra, o al menos así se indica. No se entiende nada.
“Cálculo de probabilidades en experimentos, comparaciones o investigaciones en los que sea aplicable la regla de Laplace: aplicación de técnicas básicas del conteo.”
El modelo que está en la base del cálculo de probabilidades que se trabaja en Primaria (y de la regla de Laplace) es el producto cartesiano, que, sin saber por qué, no se incluye dentro de los modelos con los que se conceptualiza la multiplicación. Sin embargo sí se incluyen las técnicas básicas de conteo. No se entiende. Si quiere saber las probabilidades de que salgan un 1 y un 2 al arrojar dos dados de seis caras cada uno, ¿qué es lo que hay que contar?
AUSENCIAS INESPERADAS O SORPRESIVAS DE CONTENIDOS.
Los números romanos.
Tal vez sea una de las ausencias menos justificadas. Nunca han faltado de ningún currículum y no se tienen noticias de que este contenido hay causado graves problemas de aprendizaje a los niños. Los números romanos no son una excentricidad, sino que forman parte de nuestra cultura. A lo largo del documento que estamos comentando se hacen continuas referencias “a la vida cotidiana” como fuente de ejercicios y de sentido de lo que se hace. Pues aquí también los números romanos tienen una vida bastante vigorosa: como marcas de las horas en muchos relojes, numeración de capítulos de libros, el nombre de los siglos, la denominación de sectores poblacionales y de regiones, etc. Un miembro del equipo de redacción del documento explicaba en la prensa la razón de la exclusión: no podían incorporar sistemas de numeración como el romano, que no están basados en la razón de proporcionalidad de sus órdenes de magnitud, porque hay muchísimos como él. Esta razón no tiene fundamento: claro que la humanidad ha ido creando sistemas para contar que no coinciden con el paradigma del nuestro, pero ninguno tiene el peso cultural y la presencia diaria en nuestra vida que tiene el sistema romano. Además de todo lo anterior, se cierra una oportunidad de mostrar la utilidad del cero en el sistema decimal, puesto que en la numeración romana el cero no existe.
Producto resuelto con números romanos. 4º de Primaria. CEIP “José Luis Poullet”, de El Puerto de Santamaría (Cádiz).
El modelo cartesiano en la multiplicación.
No aparece. Es básico para la resolución de los problemas elementales de probabilidad y combinatoria, fácil de conceptualizar por el niño, es un modelo que está detrás de las multiplicaciones geométricas… También sirve para introducir las raíces cuadradas incluso fuera del ámbito geométrico. Es lo que ocurre cuando el divisor y el cociente son iguales. Por ejemplo, “Puedo combinar mis faldas y mis blusas de 25 formas distintas. Tengo el mismo número de faldas que de blusas. ¿Cuántas faldas y cuántas blusas tengo?”
No hay operaciones con fracciones.
O no las hay cuando las fracciones tienen distinto denominador. Tampoco hay producto o división de fracciones. No se hace ninguna referencia a las fracciones con distinto denominador, ni siquiera cuando esos denominadores sean múltiplos o divisores entre sí (p.e, 2, 4 y 8; 5 y 10; etc.). En el tercer ciclo el proyecto habla de “Relación entre fracciones sencillas, decimales y porcentajes.” No se explica qué sean las fracciones sencillas, pero en la relación con los porcentajes deben tener denominador 100. La relación no se extiende a las operaciones aditivas con decimales, puesto que tal cálculo no se enseña para aplicarlo a las fracciones. Cuando en la comparación decimales-fracciones el número decimal tenga parte entera, no se va a poder establecer ninguna relación porque los niños no han trabajado las fracciones impropias. En la resolución de problemas de porcentajes no van a saber manejar las fracciones proporcionales, con lo que tendrán que recurrir, para solucionarlos, a la búsqueda del uno por ciento (como en los de proporcionalidad directa tendrán que recurrir al tanto por uno). Y así.
Los vídeos que siguen muestran la desenvoltura de los alumnos con las fracciones, y, en el caso del segundo vídeo, cómo los niños alcanzan un nivel de cálculo mental difícil de seguir.
Suma de fracciones con distintos denominadores, que no son múltiplos entre sí. 4º de Primaria. CEIP “Blasco Ibáñez”, de Alzira (Valencia).
Suma de fracciones con distintos denominadores, que son múltiplos entre sí. 4º de Primaria. CEIP “Andalucía”, de Cádiz.
En Computación no se aprende el sistema binario.
Es el lenguaje de la programación y, además, es el sistema en el que se mide la información. Es muy fácil de aprender por parte de los niños. Según nuestra experiencia, ya en 2º de Primaria la mayoría de los alumnos son capaces de entenderlo y, por tanto, de pasar cantidades de base diez a base dos, y de base dos a base diez. Pese a que en el proyecto de currículum se le da gran importancia al pensamiento computacional, los “ladrillos” que conforman ese pensamiento quedan olvidados.
De la numeración digital a la numeración decimal. 2º de Primaria del CEIP “Blasco Ibáñez”, de Alzira (Valencia).
De la numeración decimal a la numeración digital. 2º de Primaria del CEIP “Blasco Ibáñez”, de Alzira (Valencia).
Además de todo lo anterior, el patrón de crecimiento de los órdenes de magnitud del sistema binario es el mismo que se emplea en la multiplicación egipcia, y es también un gran recurso para la resolución de problemas que requieren del ingenio en el caso de los alumnos más pequeños. Si, por ejemplo, el alumno conoce la personas que viajan en un coche, en dos, en cuatro y en ocho, podrá calcular de forma muy simple cuántas viajan en siete coches, o en once o en catorce.
La ausencia del volumen y la densidad.
Es también llamativa esta ausencia. Si no hay unidades de volumen no se pueden establecer equivalencias entre estas y las de capacidad, y, consecuentemente, con las de peso. Por tanto, se hace imposible trabajar la densidad de los líquidos o de los sólidos granulados. Al fin y al cabo, la densidad no es más que el peso de distintas sustancias por una misma unidad de volumen. Es algo bastante cotidiano ver cómo el aceite flota sobre el agua, debido a su distinta densidad: pues no se va a poder aclarar esta incógnita. Otra cosa. También en la vida cotidiana son muy corrientes las referencias y usos de las medidas de volumen: muchas de las bebidas que toman los alumnos aparecen en envases cuyo contenido se expresa en cm3.
Cálculo del volumen de un cubo. 6º de Primaria. CEIP “Gallego Burín”, de Granada.
Dentro del sentido estocástico se olvidan de la mediana como medida de centralización.
En efecto. Por más que se busque no va a aparecer. Pienso que se les ha debido olvidar, porque es muy importante este valor para poder comprender la media aritmética y se constituye en un valor de referencia, respecto a la media y a la moda, para establecer la regularidad de una distribución. Lo más curioso es que en el Ciclo 3º señalan como saber básico el siguiente: “Relación y comparación de dos conjuntos de datos a partir de su representación gráfica: formulación de conjeturas, análisis de la dispersión y obtención de conclusiones.” ¿Qué análisis de dispersión van a realizar si no han trabajado ningún estadístico que exprese esa dispersión?
No hay criterios de divisibilidad, ni MCM ni MCD.
Otro gran misterio. ¿Por qué se ha suprimido todo lo referente a la divisibilidad? En el proyecto se habla mucho de la descomposición numérica de muchas maneras. Pues tal vez una de las más importantes se la salten. Por ejemplo, no se sabe cómo van a hacer cálculo mental con fracciones si no van a tener ningún procedimiento para establecer el denominador común de las mismas. Para la matemática de la ESO, es crucial que los alumnos vayan entrenados en las descomposiciones factoriales, dado el gran peso que van a alcanzar en esa Etapa. La supresión del MCM y del MCD supone una reducción efectiva muy importante del campo de resolución de problemas, actividad a la que tanta importancia se da en el documento y tantas oportunidades de ejercitación quitan.
Criba de Eratóstenes, descomposición factorial, MCM y MCD. 6º de Primaria. CEIP “Gallego Burín”, de Granada.
Desaparecen los números enteros.
Es otro contenido que desaparece respecto al currículum anterior. ¿Por qué? Pues no se sabe. Con esta pérdida se reduce el campo de estudio de los números, se pierde el sentido del número como balance, el significado del cero va a ser recortado, así como el sentido de la recta numérica. Por otro lado, los números negativos están bastante presentes en la vida cotidiana: medida de la temperatura, deudas, penalizaciones, balances de resultados deportivos, expresión del orden, etc. Desde el punto de vista puramente aritmético el trabajo con los números enteros amplía enormemente el sentido de los signos de las operaciones y los relativiza. El signo más es añadir, pero si se añaden deudas el resultado disminuye, no aumenta. Y respecto al signo menos, depende de los signos de los términos el que el resultado disminuya… o aumente. Si a una deuda le quito una parte, hay un aumento. Si a una cantidad positiva le quito una deuda, la cantidad positiva aumenta. Esta flexibilidad en la consideración de los signos de las operaciones es algo muy propio del pensamiento matemático y que, en lo que se ha comprobado, no supone un aprendizaje complicado para los niños.
Operaciones con números enteros. 6º de Primaria. CEIP “José Luis Poullet”, de El Puerto de Santa María (Cádiz).
PARA TERMINAR.
Seré breve en las reflexiones finales. Este artículo ya se ha alargado mucho.
La primera reflexión debe concluir en algo bastante claro: el nuevo proyecto de currículum contiene un recorte sustantivo de contenidos matemáticos, en general y en cada uno de los Ciclos. Anteriormente me he referido a ellos, por lo que no me volveré a repetir. Si he de añadir que tal recorte encierra falta de lógica. Por un lado, algunos de ellos me parecen arbitrarios y sin justificación (como es el caso de los números romanos). Por otro, se suprimen partes de estructuras que por ello pierden su sentido y, potencialmente, su capacidad de comprensión. Además, tal supresión en los contenidos de los dos primeros Ciclos supone recargar notablemente el último Ciclo y también los contenidos propios de Secundaria.
Cabe preguntarse por el sentido, el porqué de tal reducción. No es sencillo de intuir. Se eliminan muchos contenidos que, a primera vista, podrían parecer complejos para los alumnos, pero después, a la hora de cumplir los criterios de evaluación y las competencias que se han de desarrollar, se pide un dominio matemático superior al que se dibuja en los saberes básicos. Por ejemplo, “…el planteamiento de los grandes problemas medioambientales y sociales de nuestro mundo o problemas de consumo responsable en su realidad cercana, fomentando que el alumnado se haga participe de los mismos y desarrolle la actitud necesaria para implicarse activamente en su futuro” (Competencia específica 3) no creo que se pueda abordar con las herramientas que se proporcionan. Por referirme a un caso concreto, uno de los grandes problemas mundiales es el de la desforestación. Pues si la superficie de los bosques perdidos se proporciona en hectáreas, no va a ser fácil que el alumno se haga una cierta idea teniendo en cuenta que nadie le ha enseñado lo que es una hectárea.
La última reflexión se ocupa del alto nivel de ambigüedad con el que están redactados los saberes básicos. Parece mentira que siendo tan básicos no se sepa, en muchos de ellos, qué es lo que se quiere decir y abarcar. Pongamos ejemplos:
- La suma, resta, multiplicación y división de números naturales que se recoge en el Segundo Ciclo no precisa el grado de complejidad de cada una de ellas: ¿multiplicación por una o dos cifras?, ¿división por reparto o por agrupación, por una o dos cifras?
- En el Tercer Ciclo ya se habla de números naturales sin límites. Tampoco se le ponen a las fracciones. ¿Quiere esto decir que ya se pueden trabajar las fracciones impropias, los números mixtos, las fracciones equivalentes, las inversas, etc.? ¿Las referencias al sentido de las operaciones incluyen a las fracciones? ¿Qué son “fracciones sencillas”?
- Se emplea bastante el término “conjetura”. Debe referirse a otro significado al que normalmente se da en matemáticas a esta palabra: se refiere a afirmaciones que se presumen ciertas pero que no han sido probadas ni refutadas. La conjetura es el paso anterior al teorema. No puede ser este el sentido. En el documento se aplica por igual tanto a la Geometría (“Elaboración de conjeturas sobre propiedades geométricas…”) como a la Estadística (“Relación y comparación de dos conjuntos de datos a partir de su representación gráfica: formulación de conjeturas, análisis de la dispersión y obtención de conclusiones.”).





Deja una respuesta