«Vaya locura»

Un profesor español se queda sin palabras al ver cómo hace las divisiones su nuevo alumno inglés: «Vaya locura». Ese es el grandioso título al estilo clickbait que el diario «La Vanguardia» en su versión digital ha publicado el 15/04/2024.

Lo primero que dejo es el enlace al artículo para que cada cual saque las conclusiones que considere oportuna. Igualmente añado que lo que comento a continuación no es una crítica a Edu maestro de Primaria en mi comunidad autónoma, ni mucho menos, él muestra su asombro en su canal de tiktok y punto, cada cual es libre de asombrarse y mostrar en sus redes lo que considere oportuno. Lo que me llama la atención es que esto sea para que un periódico como la»Vanguardia» se haga eco.

Una vez dicho lo anterior, analizo brevemente de qué va el tema. Edu muestra su asombro de como un alumno que le ha llegado de inglaterra hace la división. Sin embargo, el proceso no es más que el mismo que se realiza aquí pero con una distribución diferentes de la posición del dividendo, divisor, cociente y resto. Además es el proceso que se hace en varios paises de cultura anglosajona. Pero el proceso es el mismo del tradicional de aquí, se haga poniendo los productos para restar o se hagan mentalmente las restas.

Lo que me sorprende, como indico es el eco de este periódico y la cantidad de comentarios, muy variopintos, de entre los que destaco dos que resumen la mayor parte y uno que hace referencia al ABN, por si en algun momento no está disponible el articulo.

El segundo comentario es curioso (que además tiene bastantes «corazones»), porque creen que el sistema anglosajón es más sencillo. ¡¡¡Pero si es lo mismo!!!

El último que también reproduzco, lo hago por dos razones. Una por que evidencia que cada vez hay más gente que descubre que con el ABN el aprendizaje es muchísimo más sencillo, los crios no crean ansiedad con la matemáticas y que hay otras formas mucho más lógicas de enseñar. Y la otra el la última respuesta a este comentario por parte de la misma que lo crea, en que la que por desgracia seguimos viendo opinioneso sin argumentario ni razonamiento alguno en el cual se vierte creencias infundadas y falsas como que «Cuando llegan a secundaria llegan sin saber hacer las operaciones de toda la vida». El tema para este tipo de aseveracions es sería plantearles ¿cuales son las cuentas de toda la vida? ¿Las anglosajonas, las latinas, las japonesas? ¿En la Educación Secundaria Obligatoria (ESO) continúan practicando operaciones al estilo de la Primaria, o más bien se fomenta el razonamiento lógico-matemático para abordar conceptos más complejos, relegando el cálculo a un papel secundario, similar a cómo sería la práctica de la lectura frente al análisis de textos? ¿es que aún se puede defender un sistema de cálculo tradiconalista que tanto fracaso lleva arrastrado y frustraciones en generaciones y generaciones?…😵

¿Y para cuándo se va a dar una formación como «Dios manda» y no tradicionalista en las facultades de formación del profesoraso? va siendo hora de ir adaptando la enseñanza, no al día de hoy, sino al día en el que vivirán nuestro jóven alumnado que necesitará más comprensión y razonamiento frente al mecanicismo del método tradicional.

Los comentarios…

LA ALTERNATIVA ES EL ABN, Y COMO MUESTRA…

Ya que solicitan otra forma de hacer la división en el artículo, os mostramos una de las múltiples formas (el alumando gracias al dominio de la numeración y a entender lo que está haciendo puede elegir su camino) en que el alumnado de ABN puede resolver esta misma operación. Además a continuación la comento para los que no saben de qué estamos hablando, acompañado con preguntas de razonamiento lógico matemático que son imposibles tanto en el método tradicional como en el anglosajón. Que lo disfrutéis.

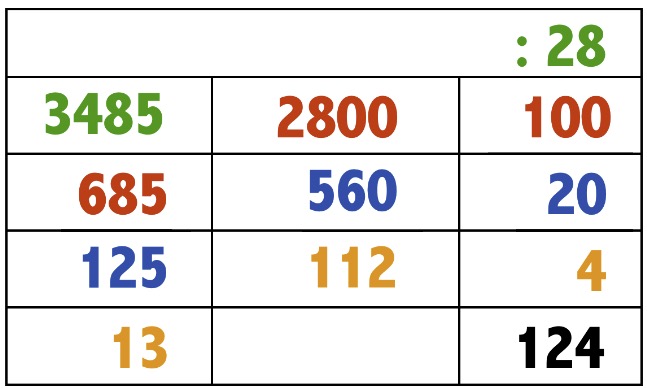
Vamos a explicarlo paso a paso. Lo primero es indicar qué son las columnas y partimos de una situación problemática, sin la cual no tiene sentido operar. Esta situación podría ser: «En una peña de 28 miembros les ha tocado 3485€. ¿A cuanto le toca a cada uno?»

La primera columna indica (dividendo) lo que hay y queda por repartir siendo la última cifra (13 en naranja) lo que no he repartido (Resto).

La columna del medio indica el dinero repartido, hasta ese momento, entre los 28 miembros de la peña.

Y la última columna (cociente) representa lo que se ha ido dando a cada miembre de la peña miembras quedaba dinero que repartir (de la primera columna). Aquí se entiende que el que reparte puede decidir la cantidad que va dando en cada reparto. Nosotros hemos escogido repartir cantidades sencillas.

Empezamos:

De primeras a cada socio se le han dado 100€ (una cantidad sencilla de repartir y de calcular) de forma que los 28 han recibido ya un total de 2800€ y aún nos han quedado por repartir 685€ (Cifras en rojo)

En el segundo reparto (en azul) hemos dado 20€. También podriamos haber dado primero 10 y luego otros 10€, de esta forma al alumando con dificultades le adaptamos la operación ¿el tradicional o anglosajón puede hace eso? Pues no😔. Con lo que hemos repardido a los 28 socios un total de otros 560€ más y nos quedán aún que repartir 125€

Y en el último reparto (en naranja) a cada socio de la peña se la han dado 4€ (si el alumno lo ve complicado puede dar primero 2€ y luego nuevamente 2€) con lo que hemos repardido a los 28 socios un total de otros 112€ más.

Finalmente cada socio ha recibido 124€ y nos quedán aún que repartir 13€ que como no hay para todos, es el resto, que se lo puede quedar el que parte y reparte 💪 o para comprar unos dulces o unas cañas 🍻.

Consideraciones finales:

• El procedimiento sencillo, lógico, se entiende y es adaptable a las necesidades del alumnado. Pedir más… imposible.
• He ido relatando el proceso paso ha paso y creo que se ha entendido . ¿Se puede hacer lo mismo enn el método tradiconal o en el anglosajón ? Pues no.
• Y vamos un poquito más allá…
  • Cuando se había repartido 100€ ¿Cuánto quedaba por repartir? ¿Cuánto recibió cada socio? ¿Cuánto se repartió en total? Pues 685€, 100€ y 2800€ respectivamente.
  • Cuando se había repartido 120€ (suma de la cifra roja y azul de la útlima columna) ¿Cuanto quedaba por repartir? ¿Cuánto recibió cada socio? ¿Cuánto se repartió en total? Pues 120€, 560€ más y 3360€ (suma de la cifra roja y azul de columna del medio) respectivamente.
  • Podríamos hacer más preguntas que se obtinen del proceso que está a la luz, pero creo que se entiende lo que queremos decir.

Lo que importa no es la mecánica (esta la hace una simple calculadora) sino entender lo que se hacer y que esto ayude a razonar. Sin comprensión no puede haber razonamiento. Si te ha resultado difícil seguir el razonamiento, la razón puede residir en el método de enseñanza que has recibido. No supongas que lo que enseñen a tus hijos no será útil en su vida adulta, ni asumas que si tú no lo entiendes, ellos tampoco lo harán.